Velotzidade

Sa velotzidade de un'ogetu est su tassu de variatzione de sa positzione sua cunfronta a unu cuadru de riferimentu e est una funtzione de su tempus. Sa velotzidade est ecuivalente a sa derivada de sa positzione sua e de sa diretzione sua de movimentu (a esèmpiu 60 km/h cara a nord). Sa velotzidade est unu cuntzetu importante in sa tzinemàtica, su ramu de sa mecànica clàssica chi descriet su movimentu de sos corpos.
Sa velotzidade est una cantidade de vetore fìsicu; siat sa grandesa chi sa diretzione sunt netzessàrias pro lu definire. Su balore assolutu iscalare (grandesa) de sa velotzidade est mutidu "lestresa", essende un'unidade coerente derivada cun una cantidade chi est mesurada in su SI (sistema mètricu) che a metros a su segundu (m/s) o comente unidade base SI de (m⋅s-1). A esèmpiu, "5 metros a su segundu" est un'iscalare, mentras "5 metros a su segundu EST" est unu vetore. Si b'at una mudada de lestresa, diretzione o ambos, tando s'ogetu tenet una velotzidade variàbile e si narat chi siat subende un'atzellerada.
Velotzidade costante vs atzellerada
[modìfica | modìfica su còdighe de orìgine]Pro tènnere una velotzidade costante, un'ogetu depet tènnere una lestresa costante in una diretzione costante. Sa diretzione costante vìnculat s'ogetu a su movimentu in unu percursu deretu, tando una velotzidade costante signìficat movimentu in lìnia reta a una lestresa costante.
A esèmpiu, una màchina chi si movet in manera costante a 20 chilòmetros a s'ora in unu percursu tzirculare tenet una lestresa costante, ma non tenet una velotzidade costante ca sa diretzione sua càmbiat. Tando, sa màchina est cunsiderada in fase de atzellerada.
Distintzione intre velotzidade e lestresa
[modìfica | modìfica su còdighe de orìgine]
Sa lestresa descriet petzi cantu lestru un'ogetu s'est movende, mentras sa velotzidade dat siat sa lestresa sa diretzione de movimentu de s'ogetu.[1] Si si narat chi una màchina biàgiat a 60 km/h, sa lestresa sua est istada ispetzificada. Nointames, si si narat chi sa màchina si movet a 60 km/h cara a nord, sa velotzidade sua est istada como ispetzificada.
Sa diferèntzia manna si podet notare cando pigamus in cunsideru su movimentu a fùrriu a unu chircu. Cando carchi cosa si movet in unu percursu tzirculare (a lestresa costante, bide subra) e torrat a su puntu suo de partèntzia, sa velotzidade mèdia sua est zero ma sa lestresa mèdia sua benit agatada dividende sa tzircunferèntzia de su chircu pro su tempus impreadu pro si mòere a fùrriu a su chircu. Custu ca sa velotzidade mèdia benit contada cunsiderende petzi su mudamentu intre sos puntos initziale e finale mentras sa lestresa mèdia cunsìderat isceti sa distàntzia totale cursada.
Ecuatzione de su motu
[modìfica | modìfica su còdighe de orìgine]Velotzidade mèdia
[modìfica | modìfica su còdighe de orìgine]Sa velotzidade est definida comente a sa resone de sa mudada de positzione cunfronta a su tempus, chi si podet fintzas indicare che a sa velotzidade istantànea pro pònnere ènfasi in sa distintzione cun sa velotzidade mèdia. In unas cantas aplicatziones diat pòdere èssere netzessària sa "velotzidade mèdia" de un'ogetu, est a nàrrere sa velotzidade costante chi diat frunire su matessi mudamentu risultante comente una velotzidade variàbile in su matessi tantu de tempus, v(t), pro unu tzertu perìodu de tempus Δt. Sa velotzidade mèdia podet èssere rapresentada comente:
Sa velotzidade mèdia est semper prus minore o uguale a sa lestresa mèdia de un'ogetu. Custu si podet bìdere realizende chi mentras sa distàntzia creschet semper in manera istrinta, su mudamentu podet crèschere o diminuire de mannesa e cambiare diretzione.
In tèrmines de unu gràficu de mudamentu (x vs. t), sa velotzidade istantànea (o, in manera simpre, velotzidade) podet èssere pensada comente a sa pendèntzia de sa lìnia tangente a sa curva in cale si siat puntu e sa lestresa mèdia comente a pendèntzia de sa lìnia secante intre duos puntos cun coordinadas t pares a sos lìmites de su perìodu de tempus pro sa velotzidade mèdia.
Sa velotzidade mèdia est sa matessi de sa lestresa mediada in su tempus, est a nàrrere sa mèdia ponderada in su tempus sua, chi podet èssere contada che a s'integrale temporale de sa lestresa:
ue podimus identificare
e
Velotzidade istantànea
[modìfica | modìfica su còdighe de orìgine]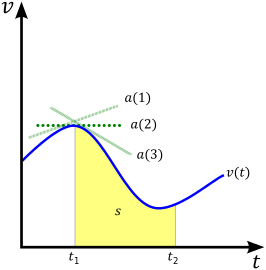
Si cunsideramus v che a sa velotzidade e x che a su vetore de mudamentu (cambiadu de positzione), tando podimus espressare sa velotzidade (istantànea) de una partighedda o ogetu, in onni momentu t, comente derivada de sa positzione cunfronta a su tempus:
Dae custa ecuatzione derivada, su casu unidimensionale faghet bìdere chi s'àrea in suta de una velotzidade cunfronta a su tempus (gràficu v vs t) est su mudamentu, x. In tèrmines de càrculu, s'integrale de sa funtzione de velotzidade v(t) est sa funtzione de mudamentu x(t). In sa figura, custa currispondet a s'àrea groga in suta de sa curva cun eticheta s (s una notatzione alternativa pro su mudamentu).
Sigomente sa derivada de sa positzione cunfronta a su tempus dat sa mudada de positzione (in metros) divididu pro sa mudada de tempus (in segundos), sa velotzidade benit mesurada in metros a su segundu (m/s). Cando chi su cuntzetu de velotzidade istantànea potzat, in comintzu, pàrrere malu a l'intuire, lu si podet pensare comente a sa velotzidade chi s'ogetu at a impreare sighende a biagiare si acabbaret de atzellerare in cussu momentu.
Raportu cun s'atzellerada
[modìfica | modìfica su còdighe de orìgine]Mancari sa velotzidade siat definida comente a sa resone de sa mudada de positzione, est comunu a s'sispissu incumentzare cun un'espressione pro s'atzellerada de un'ogetu. Comente si bidet dae sas tres lìnias tangentes birdes in sa figura, s'atzellerada istantànea de un'ogetu in unu puntu in su tempus est sa pendèntzia de sa lìnia tangente a sa curva de unu gràficu v(t) in cussu puntu. In àteras paràulas, s'atzellerada est definida comente sa derivada de sa lestresa cunfronta a su tempus:
Dae cue, podimus otènnere un'espressione pro sa velotzidade comente s'àrea in suta de unu gràficu a(t) de atzellerada cunfronta a su tempus. Comente a subra, custu si faghet impreende su cuntzetu de integrale:
Atzellerada costante
[modìfica | modìfica su còdighe de orìgine]S'in casu ispetziale de s'atzellerada costante, sa velotzidade si podet istudiare impreende sas ecuatziones de su motu. Cunsiderende a comente a uguale a unu vetore arbitràriu costante, est banale dimustrare chi
cun v comente sa velotzidade a su tempus t e u comente sa velotzidade a su tempus t = 0. Cumbinende custa ecuatzione cun s'ecuatzione de su motu x = ut + at2/2, est possìbile currelare su mudamentu e sa velotzidade mèdia comente
- .
Est fintzas possìbile derivare un'espressione pro sa velotzidade indipendente dae su tempus, nòdida comente a ecuatzione de Torricelli, comente custa:
ue v = |v|Template:Math etz.
Sas ecuatziones de subra sunt bàlidas siat pro sa mecànica newtoniana chi pro sa relatividade ispetziale. Ue sa mecànica newtoniana e sa relatividade ispetziale diferint, est in su modu in cale diversos osservadores descrient sa matessi situatzione. Pro l'acrarire prus a sa minuda, in sa mecànica newtoniana totu sos osservadores cunsertant in su balore de t e sas règulas de mudadura pro sa positzione creant una situatzione in ue totu sos osservadores no-atzellerantes descrient s'atzellerada de un'ogetu cun sos matessi balores. No est beru mancu pro sa relatividade ispetziale. In àteras paràulas, si podet cunsiderare petzi sa velotzidade relativa.
Cantidades chi dipendent dae sa velotzidade
[modìfica | modìfica su còdighe de orìgine]S'energia tzinètica de un'ogetu in movimentu dipendet dae sa velotzidade sua e est dada dae s'ecuatzione
disconnoschende sa relatividade ispetziale, ue Ek est s'energia tzinètica e m est sa massa. S'energia tzinètica est una grandesa iscalare in cantu dipendet dae su cuadradu de sa lestresa, nointames una cantidade currelada, cantidade de movimentu, est unu vetore e nd'est definidu dae
In sa relatividade ispetziale, su fatore adimensionale de Lorentz aparit in manera fitiana, e est dadu dae
ue γ est su fatore de Lorentz e c est la lestresa de sa lughe.
Sa velotzidade de fua est sa lestresa mìnima chi serbit a un'ogetu balìsticu pro chi potzat fuire dae unu corpus massitzu che a sa Terra. Rapresentat s'energia tzinètica chi, si agiunta a s'energia potentziale gravitatzionale de s'ogetu, (chi est semper negativa) est uguale a zero. Sa fòrmula generale pro sa velotzidade de fua de un'ogetu a una distàntzia r de su tzentru de unu praneta cun massa M est
ue G est sa costante gravitatzionale e g est s'atzelerada gravitatzionale. Sa velotzidade de fua de sa superfìtzie terrestre est de belle 11 200 m/s e est indipendente dae sa diretzione de s'ogetu. Custu faghet in manera chi "velotzidade de fua" siat un'agigu impròpriu, ca su tèrmine prus adatu diat èssere "lestresa de fua": cale si siat ogetu chi sègudat una velotzidade de custa mannesa, in manera indipendente de s'atmosfera, at a lassare sa bighinàntzia de su corpus de base fintzas a cando no at a addobiare carchi cosa in su percursu suo.
Velotzidade relativa
[modìfica | modìfica su còdighe de orìgine]Sa velotzidade relativa est una medida de sa velotzidade intre duos ogetos determinada in unu sistema de coordinadas sìngulu. Sa velotzidade relativa est fundamentale in sa fìsica clàssica e moderna, dae chi medas sistemas in fìsica s'òcupant de su motu relativu de duas o prus partigheddas. In sa mecànica newtoniana, sa velotzidade relativa est indipendente de sa curnisa de riferimentu inertziale seberada. Custu no est prus su casu de sa relatividade ispetziale in ue sas velotzidades dipendent dae su sèberu de su fotogramma de riferimentu.
Si un'ogetu A si moet cun su vetore de velotzidade v e un'ogetu B cun su vetore de velotzidade w, tando sa velotzidade de s'ogetu A cunfronta a s'ogetu B est definida comente sa diferèntzia intre sos duos vetores de velotzidade:
A sa matessi manera sa velotzidade relativa de s'ogetu B chi si moet cun sa veloztidade w, relativa a s'ogetu A chi si moet cun sa velotzidade v est:
A su sòlitu benit seberada sa trama inertziale in ue s'ùrtimu de sos duos ogetos mentovados est in pasu.
Velotzidades iscalares
[modìfica | modìfica su còdighe de orìgine]In su casu unidimensionale,[2] sas velotzidade sunt iscalares e s'ecuatzione est:
- , si sos duos ogetos si sunt movende in diretziones opostas, o:
- , si sos duos ogetos si sunt movende in sa matessi diretzione.
Coordinadas polares
[modìfica | modìfica su còdighe de orìgine]In coordinadas polares, una velotzidade bidimensionale est descrita dae una velotzidade radiale, definida che a su cumponente de sa velotzidade a largu de, o cara a, s'orìgine (nòdida fintzas comente a velotzidade currigida), e una velotzidade angulare, chi est su tassu de rotatzione a fùrriu a s'orìgine (cun cantidades positivas chi rapresentant sa rotatzione in sensu antioràriu e cantidades negativas chi rapresentant sa rotatzione in sensu oràriu, in unu sistema de coordinadas cara a destra).
Sas velotzidades radiales e angulares podent èssere derivadas dae sos vetores de velotzidade e mudamentu cartesianos mediante sa decumpositzione de su vetore de velotzidade in cumponentes radiales e trasversales. Sa velotzidade trasversale est su cumponente de sa velotzidade longu unu chircu atzentradu in s'orìgine.
ue
- est sa velotzidade transversale
- est sa velotzidade radiale.
Sa mannaria de sa velotzidade radiale est suprodutu iscalare de su vetore de velotzidade e su vetore unitàriu in sa diretzione de su mudamentu.
ue
- est mudamentu.
Sa mannaria de sa velotzidade trasversale est cussa de su produtu vetoriale de su vetore unitàriu in sa diretzione de su mudamentu e de su vetore de velotzidade. Est fintzas su produtu de sa velotzidade angulare \omega\ e de sa grandesa de su mudamentu.
in manera chi
Su momentu angulare in forma iscalare est sa massa multiplicada pro sa distàntzia a s'orìgine multiplicada pro sa velotzidade trasversale o, in manera ecuivalente, sa massa pro sa distàntzia cuadrada multiplicada pro sa velotzidade angulare. Sa cunventzione de sinnu pro su momentu angulare est sa matessi de cussa pro sa velotzidade angulare.
ue
- est sa massa
S'espressione est connota comente momentu de inèrtzia. Si sas fortzas sunt in sa diretzione radiale petzi cun una dipendèntzia cuadràtica furriada, comente su casu de un'òrbita gravitatzionale, su momentu angulare est costante e sa velotzidade trasversale est proportzionale a s'imbesse a sa distàntzia, sa velotzidade angulare est proportzionale a s'imbesse a sa distàntzia a su cuadradu e sa velotzidade cun sa cale s'àrea benit mundada est costante. Custas relatziones sunt connotas che a sas leges de Keplero de su motu planetàriu.
Riferimentos
[modìfica | modìfica su còdighe de orìgine]- ↑ (EN) Vector analysis; a text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs by Edwin Bidwell Wilson., in HathiTrust. URL consultadu s'11 trìulas 2022.
- ↑ (EN) The Open Door Web Site : IB Physics : RELATIVITY : RELATIVE VELOCITY, in www.saburchill.com. URL consultadu s'11 trìulas 2022 (archiviadu dae s'url originale su 26 santandria 2022).
Bibliografia
[modìfica | modìfica su còdighe de orìgine]- (EN) David Halliday, Robert Resnick e Jearl Walker, Fundamentals of physics, Milton, John Wiley, 2020, ISBN 978-0-7303-8287-4, OCLC 1277393734.
Ligàmenes esternos
[modìfica | modìfica su còdighe de orìgine]- (EN) JPA, Velocity and Acceleration, in jaredzone.info. URL consultadu s'11 trìulas 2022.
- (EN) Introduction to Mechanisms, in Carnegie Mellon University. URL consultadu s'11 trìulas 2022.
| Controllu de autoridade | BNF (FR) cb119762787 (data) · GND (DE) 4020574-5 · LCCN (EN) sh85126486 · NKC (EN, CS) ph872791 |
|---|

































